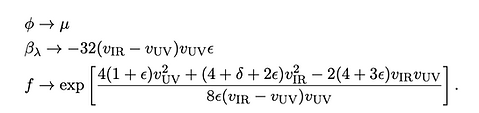Primordial Black Holes from first-order Phase Transitions

Published in Phys.Rev.D 110 (2024) 4, 043514 - e-Print: 2305.04942 [hep-ph]
Our universe underwent several important changes in its early age, known as cosmological phase transitions. Some of these transitions happened when particles like quarks and gluons became confined, or when the Higgs field changed in density. There may have been other phase transitions related to the mass of neutrinos or the axion of the strong force. Some of these phase transitions could have arisen through bubble nucleation, similar to boiling water.
Did the universe "boil" for a long time?
Our new research provides evidence that phase transitions that boiled longer than 15% of the age of the universe at that time would have produced a large abundance of black holes.
Those black holes arise from the collapse of "late-bloomers", which are causal regions that form bubbles later than the background.
Those black holes of primordial origin could be detectable with current and future technologies.


Published in: Phys.Lett.B 855 (2024) 138800 • e-Print: 2311.13640 [hep-ph]
For PBHs production to be efficient, two rather extreme conditions must be satisfied simultaneously:
In the figure below, we compare the tunneling bounce action for two types of scalar potential: 1) polynomial potential and 2) nearly-conformal potential.
The two parameters α and β/H can be calculated from the temperature dependence of the bounce action. As shown below, PTs driven by polynomial potential have a bounce action which quickly drops with temperature as a power law S3 /T ∝ T^n. Instead, PTs driven by nearly-conformal potentials have a bounce action which only slowly decreases logarithmically S3/T ∝ 1/ log^n(T ). This explains while nearly-conformal potentials can easily feature large α and small β/H parameters, while polynomial potentials typical don’t.

Hence nearly-scale-invariant models can easily present the two necessary conditions to the formation of PBHs. In 2311.13640, I have studied the minimial scale-invariant extension of the Standard Model (SM). One scalar field charged under a dark U(1) gauge group is added to the SM. We assume that all mass scales vanish a tree level. The electroweak scale emerges by dimensional transmutation due to the 1-loop quantum correction, as predicted by Coleman and E. Weinberg (CW) in 1973. The CW potential of the U(1) scalar field plus its thermal mass read:
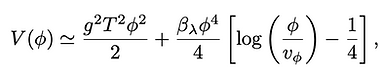
The logarithm leads to supercooling, meaning that the nucleation temperature Tn is exponentially smaller than the critical temperature Tc:

The logarithm dependence also leads the PT to occur with a slow rate of completion β, almost comparable to the expansion rate H:
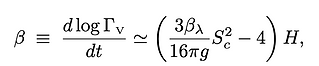
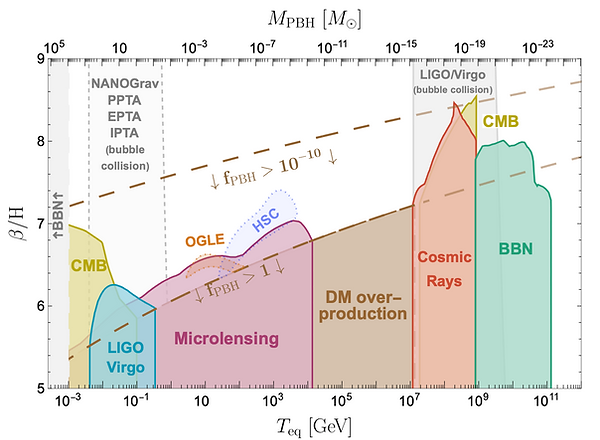
The last two conditions are the two necessary conditions for efficient primordial black hole production. Thoses PBH can leave signatures in a variety of probes (microlensing, Dark Matter, cosmic-rays, CMB, BBN):
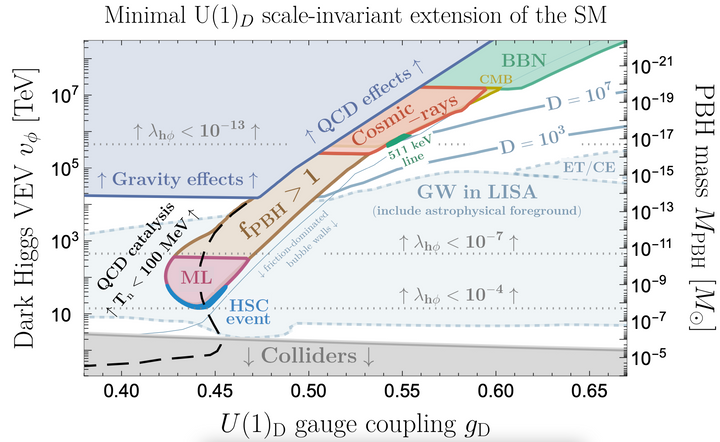
Those results are not restricted to the weakly-coupled Coleman-Weinberg (CW) 1-loop correction:

In fact, the CW potential belongs to the much wider class of scale-invariant extensions of the SM. First of all, they can also arise in strongly-coupled sectors when the explicit breaking of conformal invariance is sufficiently small at confinement, so that a light pseudo-Goldstone boson exists in the spectrum, the dilaton σ:
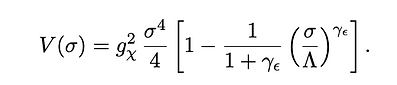
In the limit of vanishing anomalous scaling dimension γε → 0, the light dilaton model maps to the CW model as follows:
Second of all, they can arise from 5D holographic warped description. Using AdS/CFT correspondence, the strongly-coupled 4D theory discussed above can be mapped to a weakly-coupled 5D theory with AdS5 metric. For definiteness, we can consider the Randall-Sundrum scenario, which is a slice of AdS5 bounded by two branes, whose interdistance is stabi- lize by the Goldberger-Wise mechanism. The potential for the radion μ encoding the distance between the two branes reads:
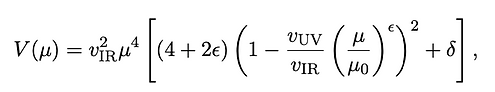
where vIR and vUV are the vev of the Goldberger-Wise scalar field on the IR and UV brane in unit of its mass m, and ε = (mL)2/4 where L is the AdS radius. In the limit ε → 0, the radion potential takes for form of the CW potential with: